Since it's a bit of a pain to make beautiful in the email itself, see the attached PDF. Here's the text of that:
Claim
The bin-wise average of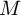 DFTs of
consecutive, non-overlapping input samples is the same as the DFT of
the sample-wise averaged, consecutive, non-overlapping input
vectors.
DFTs of
consecutive, non-overlapping input samples is the same as the DFT of
the sample-wise averaged, consecutive, non-overlapping input
vectors.Proof
As mention in the claim, we average over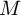 DFTs. Let
the length of the individual DFT be
DFTs. Let
the length of the individual DFT be 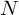 .
.Let us consider a complex input signal
![$x[n]$](pngIHGHUxDCxd.png) ,
with
,
with  being the
non-negative index, that exists for the whole observation, hence
being the
non-negative index, that exists for the whole observation, hence 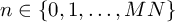 .
.Lets use the same definition of the discrete Fourier transform as is used in FFTW[1], so that the first DFT
 would yield in bin
would yield in bin 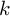 :
: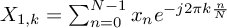 .
.Introducing the average DFT
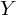 , we see
that
, we see
that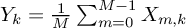
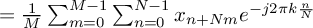 .
.With the sums above being finite, we can change their order:
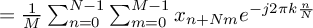
The exponential term doesn't depend on
 ,
and hence can be extracted from the inner sum.
,
and hence can be extracted from the inner sum.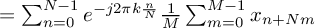

Notice that

is the sample average over
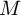 consecutive, non-overlapping sample vectors of length
consecutive, non-overlapping sample vectors of length 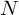 .
.
SNR considerations
Let us consider the job of the DFT to find the coefficients that you'd have to write in front of the individual series representing an
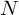 long
complex oscillation with frequency
long
complex oscillation with frequency 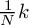 , i.e. the set of series
, i.e. the set of series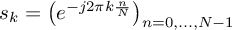 .
.All the
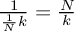 -periodic oscillations are also
-periodic oscillations are also
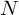 -periodic
(by definition of periodicity).
-periodic
(by definition of periodicity).Hence, in consecutive vectors of length
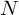 , if
you add up the elements with the same index, and the observed signal
is periodic, you simply get the averaging factor
, if
you add up the elements with the same index, and the observed signal
is periodic, you simply get the averaging factor 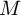 as the
factor between the individual vector and the sum of
as the
factor between the individual vector and the sum of 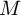 vectors.
vectors.Now, remember that the purpose of averaging the DFTs was to enhance SNR by
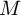 . That's
exactly what happens when you average the input signal, too.
. That's
exactly what happens when you average the input signal, too.[1] FFTW, the Fastest Fourier Transform in the West, What FFTW Really Computes: The 1d Discrete Fourier Transform (DFT),
http://www.fftw.org/doc/The-1d-Discrete-Fourier-Transform-_0028DFT_0029.html#The-1d-Discrete-Fourier-Transform-_0028DFT_0029
On 09.11.2015 11:55, Daniele Nicolodi
wrote:
On 06/11/15 19:01, madengr wrote:Marcus Müller-3 wroteHi Lou, that's a pretty good application of the spectrum, I agree. One could certainly modify the freq_sink to do that, however, as it is now, the PSD calculation (based on the fft result) is done in a single VOLK kernel, 32fc_s32f_x2_power_spectral_density_32, which probably has some performance advantages, so changing that would mean to either abandon that benefit or introduce a new "processing path" inside the frequency sink. I'm a bit confused, though: The DFT is a linear operation. So averaging k FFT vectors (linear operation) before or after the DFT wouldn't make a difference, because, with
being our DFT length-sized input sample vectors. You should be able to do
with a stream to vector->add block combination in front of the normal frequency sink.
Hmm.. maybe it is. I have done it in (shudder) LabView and it's nice since noise reduces at 1/N instead of 1/sqrt(N); N is number of averages. Maybe I'll try it tonight with just discrete blocks to compare them side by side. Just something that can't be done with a normal spectrum analyzer.Why does that hold true? I don't think it is possible, at least in the general case. Cheers, Daniele _______________________________________________ Discuss-gnuradio mailing list address@hidden https://lists.gnu.org/mailman/listinfo/discuss-gnuradio